In mechanics and physics, simple harmonic motion is a type of periodic motion where the restoring force is directly proportional to the displacement. It can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. In addition, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum as well as molecular vibration. Simple harmonic motion is typified by the motion of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's Law. The motion is sinusoidal in time and demonstrates a single resonant frequency. In order for simple harmonic motion to take place, the net force of the object at the end of the pendulum must be porportional to the displacement.
The following physical systems are some examples of simple harmonic oscillator.
Mass on a spring
A mass m attached to a spring of spring constant k exhibits simple harmonic motion in closed space. The equation
T= 2 \pi{\sqrt{\frac{m}{k}}}
shows that the period of oscillation is independent of both the amplitude and gravitational acceleration.

Simple harmonic motion shown both in real space and phase space. The orbit is periodic. (Here the velocity and position axes have been reversed from the standard convention in order to align the two diagrams)
In the diagram a simple harmonic oscillator, comprising a mass attached to one end of a spring, is shown. The other end of the spring is connected to a rigid support such as a wall. If the system is left at rest at the equilibrium position then there is no net force acting on the mass. However, if the mass is displaced from the equilibrium position, a restoring elastic force which obeys Hooke's law is exerted by the spring.
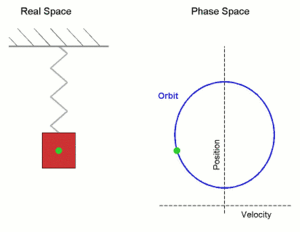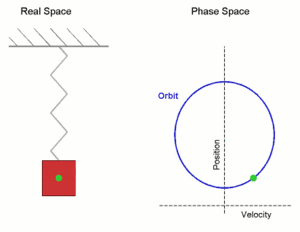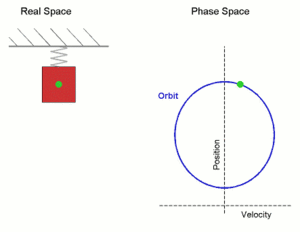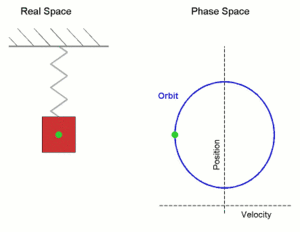
An undamped spring�mass system undergoes simple harmonic motion.
In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The period of a mass attached to a pendulum of length � with gravitational acceleration g is given by
T = 2 \pi \sqrt{\frac{\ell}{g}}
This shows that the period of oscillation is independent of the amplitude and mass of the pendulum but not the acceleration due to gravity (g), therefore a pendulum of the same length on the Moon would swing more slowly due to the Moon's lower gravitational acceleration.

The motion of an undamped Pendulum approximates to simple harmonic motion if the amplitude is very small relative to the length of the rod.


