Image processing Bilinear Interpolation Algorithm
by THavamani[ Edit ] 2013-08-13 14:41:43
What is Bilinear interpolation ?
Bilinear interpolation is used when we need to know values at random position on a regular 2D grid. Note that this grid can as well be an image or a texture map.
For Example:
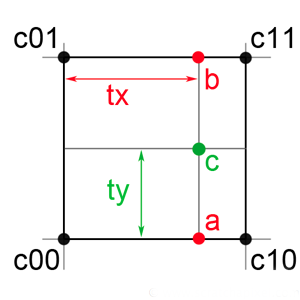we are interested in finding a value at the location marked by the green dot (c which has coordinates cx, cy). To compute a value for c we will first perform two linear interpolations (see introduction) in one direction (x direction) to get b and a. To do so we will linearly interpolate c00-c10 and c01-c11 to get a and b using tx (where tx=cx). Then we will linearly interpolate a-b along the second direction (y-axis) to get c using ty (ty=cy). Whether you start interpolating the first two values along the x-axis or along the y-axis doesn't make any difference. In our example we start by interpolating c00-c10 and c01-c11 to get a and b. We could as well have interpolated c00-c01 and c10-c11 using ty then interpolated the result (a and b) using tx. To make the code easier to debug and write though it is recommended to follow the axis order (x, y and z for trilinear interpolation).
Bilinear interpolation Algorithm :
template<typename T>
T bilinear(
const T &tx,
const T &ty,
const T &c00,
const T &c10,
const T &c01,
const T &c11)
{
#if 1
T a = c00 * (T(1) - tx) + c10 * tx;
T b = c01 * (T(1) - tx) + c11 * tx;
return a * (T(1) - ty) + b * ty;
#else
return (T(1) - tx) * (T(1) - ty) * c00 +
tx * (T(1) - ty) * c10 +
(T(1) - tx) * ty * c01 +
tx * ty * c11;
#endif
}
template<typename T>
void testBilinearInterpolation()
{
int imageWidth = 512;
int gridSizeX = 9, gridSizeY = 9;
Vec3 *grid2d = new Vec3[(gridSizeX + 1) * (gridSizeY + 1)];
for (int j = 0, k = 0; j <= gridSizeY; ++j) {
for (int i = 0; i <= gridSizeX; ++i, ++k) {
grid2d[j * (gridSizeX + 1) + i] = Vec3(drand48(), drand48(), drand48());
}
}
Vec3 *imageData = new Vec3[imageWidth*imageWidth], *pixel = imageData;
for (int j = 0; j < imageWidth; ++j) {
for (int i = 0; i < imageWidth; ++i) {
T gx = i / T(imageWidth) * gridSizeX;
T gy = j / T(imageWidth) * gridSizeY;
int gxi = int(gx);
int gyi = int(gy);
const Vec3 & c00 = grid2d[gyi * (gridSizeX + 1) + gxi];
const Vec3 & c10 = grid2d[gyi * (gridSizeX + 1) + (gxi + 1)];
const Vec3 & c01 = grid2d[(gyi + 1) * (gridSizeX + 1) + gxi];
const Vec3 & c11 = grid2d[(gyi + 1) * (gridSizeX + 1) + (gxi + 1)];
*(pixel++) = bilinear >(gx - gxi, gy - gyi, c00, c10, c01, c11);
}
}
saveToPPM("./bilinear.ppm", imageData, imageWidth, imageWidth);
delete [] imageData;
}
Input Image:
Output Image:
Advantage of bilinear interpolation:
Advantage of bilinear interpolation is that it is fast and simple to implement. However, If you look at the second image from figure 2, you will see that bilinear interpolation creates some patterns which are not necessarily acceptable depending on what you intend to use the result of the interpolation for. If you need a better result you will need to use more advanced interpolation techniques involving interpolation functions of degree two or more.
